Higher brain functions, such as sensory information processing and the attendant complexities of learning, memory storage, and pattern recognition, rely on the orchestrated interplay of a large number of neurons. Through their collective dynamics, structure emerges in large-scale spatiotemporal brain activity and information can be introduced into the nervous system.

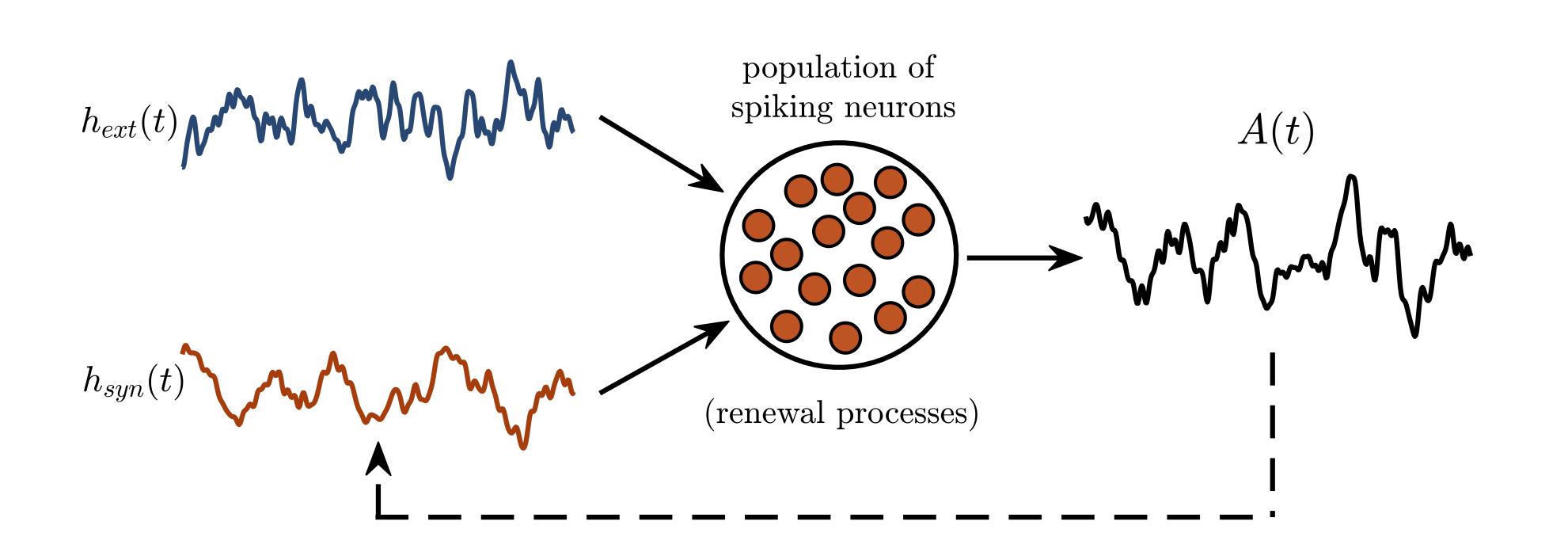
A major goal of neuroscience, statistical physics, and nonlinear dynamics is to understand how brain function arises from the collective dynamics of networks of spiking neurons. This challenge has been chiefly addressed through large-scale numerical simulations. Alternatively, researchers have formulated mean-field theories to gain insight into macroscopic states of large neuronal networks in terms of the collective firing activity of the neurons, or the firing rate.

To describe the collective dynamics of large populations of neurons, one often resorts to traditional firing-rate, or neural-mass, models. These models are low-dimensional and therefore analytically tractable. But they are also heuristic and cannot capture more complex dynamics of stochastic spiking neurons. Fundamentally, these theories have not succeeded in establishing an exact correspondence between the firing rate of the network and the underlying microscopic state of the spiking neurons. This has largely constrained the range of applicability of such macroscopic descriptions, particularly when trying to describe neuronal synchronization.

Here, we will present a systematic reduction of the population activity of general renewal-type neurons that can account for neuronal refractoriness and spike synchronization dynamics.

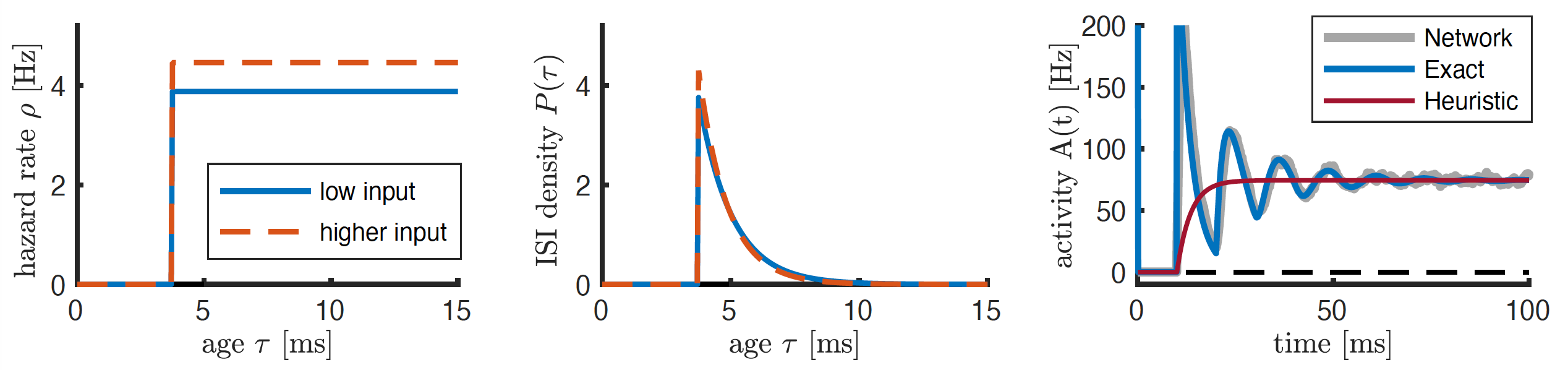
A single neuron is uniquely characterized through the probability to elicit a spike in the next instant in time, given its age (i.e. the time elapsed since its last spike) and some input. This spiking probability is proportional to the so-called hazard rate, depicted on the left. The hazard rate, in turn, is closely related to the interspike interval (ISI) density P, here shown in the middle. Assuming an infinitely large population of similar neurons, we can group all those neurons together that have the same age. The resulting neuron density is called the refractory density, and follows a particular continuity equation. From this refractory density equation, one can readily deduce the population activity that shows some oscillatory behavior as a response to a step-input current, see the blue curve in the right panel. There, we also plotted the population activity for a network of 10’000 neurons (gray) as well as the dynamics obtained with a traditional firing rate model (red), which however is unable to capture the ringing behavior of the population response.

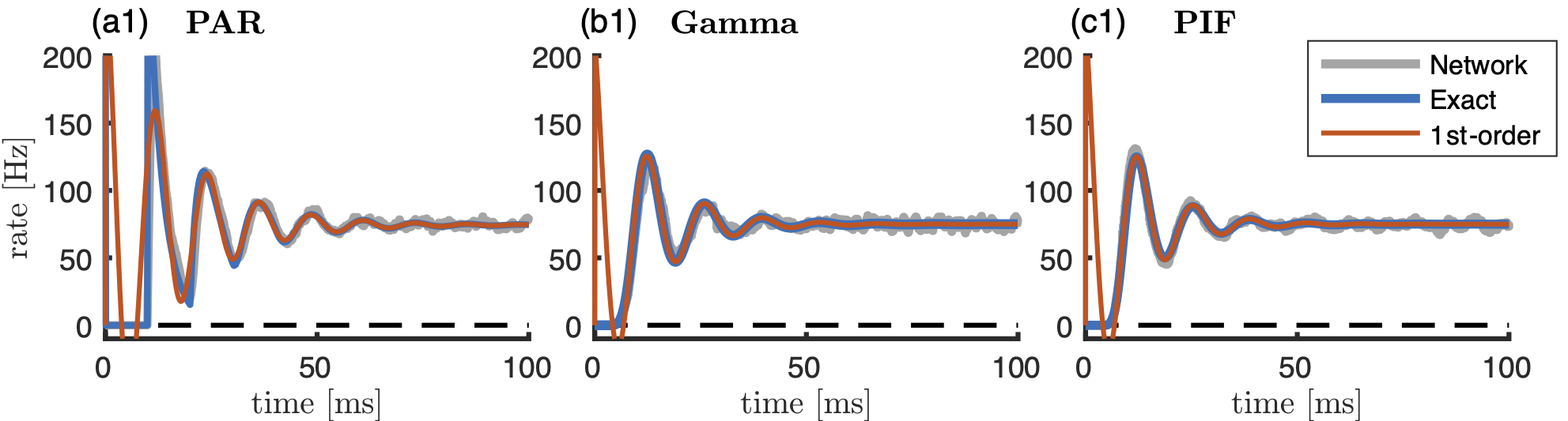
In order to derive accurate low-dimensional firing rate models, we perform a spectral decomposition, which is based on an eigenmode expansion, of the refractory density equation. Already a first-order approximation yields an accurate firing rate model that captures spike synchronization effects and fast transient dynamics at stimulus onset, see the figure at the bottom for three different neuron types. The characteristic time scales of the system, such as the decay rate and the frequency of the ringing behavior, can be determined through a simple eigenvalue formula in terms of the ISI density P of the renewal process. The eigenvalue formula thus directly links microscopic neuronal properties to observed macroscopic behavior. Last, we would like to note that our approach generalizes previous spectral methods for Fokker-Planck equations to arbitrary renewal models and we obtain equivalent firing rate dynamics for integrate-and-fire models driven by white noise in an alternative, but more elegant way.